Решить задачу
| 24.04.2025, 19:33 | |
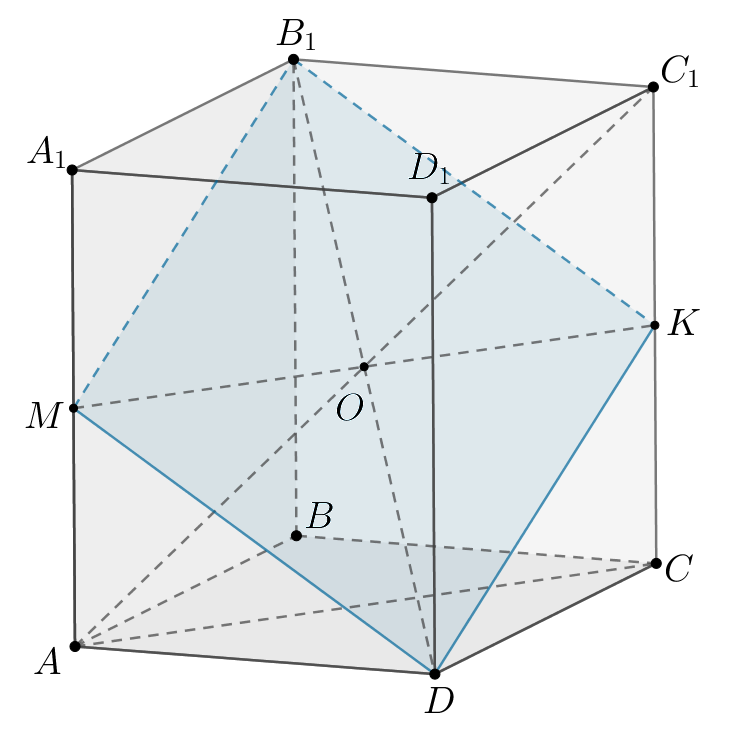
В прямоугольном параллелепипеде а) Докажите, что б) Найдите расстояние от точки | |
|
| |
| Просмотров: 13 | | |
известно, что 
Через точки 
и 
параллельно 
проведена плоскость, пересекающая ребро 
в точке 
— середина 
до плоскости сечения.| Всего комментариев: 1 | |
0
а) Назовем плоскость, проходящую через
 и  параллельно  плоскостью  Рассмотрим плоскость  Эта плоскость содержит  и пересекает  в середине — точке  Сечение параллелепипеда этой плоскостью — прямоугольник  Проведем через точку  прямую  Тогда  Следовательно,  — сечение параллелепипеда плоскостью   Ответ: Так как
 — середина  то  — точка пересечения диагоналей параллелепипеда, следовательно,  — середина диагонали  Значит, по теореме Фалеса для  где  имеем:  — середина  Что и требовалось доказать. б) Рассмотрим многогранник  Его объем равен половине объема параллелепипеда:  Если из этого объема вычесть объемы пирамид  и  каждый из которых равен  то получим объем пирамиды  С другой стороны, если  — расстояние от точки  до плоскости  то объем пирамиды  равен  Следовательно  Из этого равенства можно найти  если найти площадь сечения. По теореме Пифагора  Пусть  Тогда по теореме косинусов из   Тогда  Так как  — параллелограмм (плоскость  пересекает параллельные грани параллелепипеда по параллельным прямым), то получаем  Следовательно,  | |
