Решить задачу
| 24.04.2025, 19:36 | |
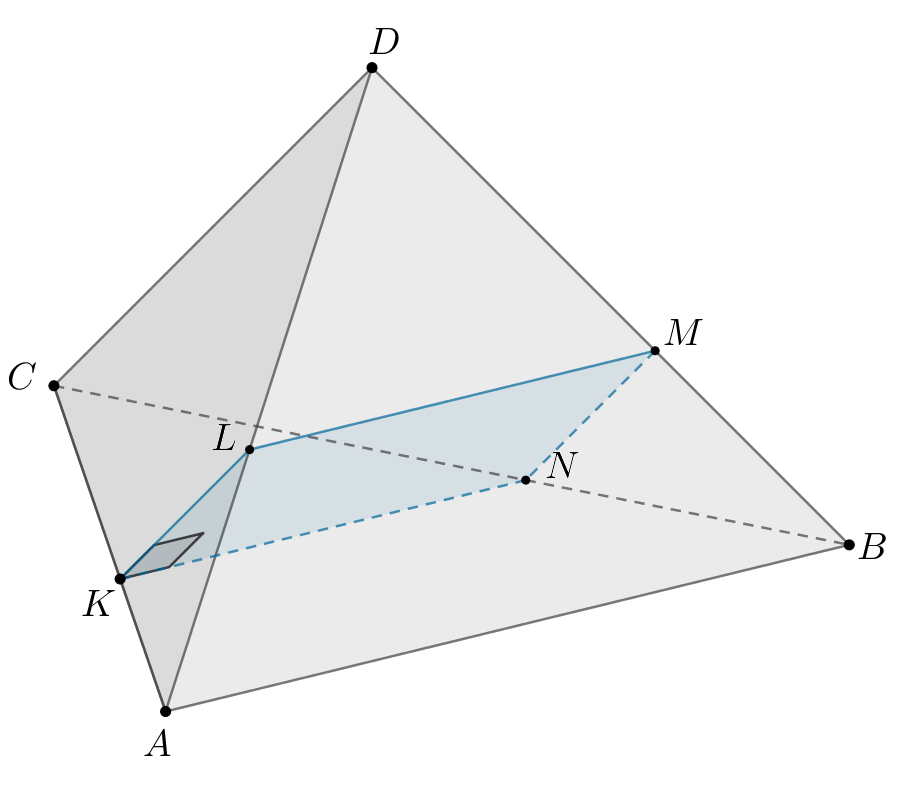
Bсе боковые ребра четырехугольной пирамиды a) Докажите, что высота пирамиды, опущенная из вершины б) В каком отношении, считая от точки | |
|
| |
| Просмотров: 25 | | |
равны 
— стороне основания 
Стороны 
и 
вдвое меньше стороны 
проходит через середину 
плоскость 
делит высоту пирамиды, если 
— середина 
а точка 
делит ребро 
в отношении 
считая от точки 
| Всего комментариев: 2 | |
0
а) Так как
 — квадрат, то имеем:  Докажем, что  Аналогично будет доказываться, что  Рассмотрим плоскости   и  Их линии пересечения   и  либо параллельны друг другу, либо пересекаются в одной точке. Так как две из трех линий  и  друг другу параллельны, то и третья линия  им параллельна. Следовательно,  Значит и   Из параллельности выше следует, что  и  Следовательно,  Так как  — квадрат, то  следовательно,  Что и требовалось доказать.
0
б) Докажем следующее утверждение. Если
 и  — противоположные ребра тетраэдра,  — расстояние между ними,  — угол между ними, то объем этого тетраэдра равен  Рассмотрим призму  в основании которой лежит четырехугольник  диагонали которого соответственно равны и параллельны двум противоположным ребрам данного тетраэдра:  Тогда расстояние между основаниями призмы равно  Значит, объем этой призмы равен   Распишем, чему равен объем данного тетраэдра    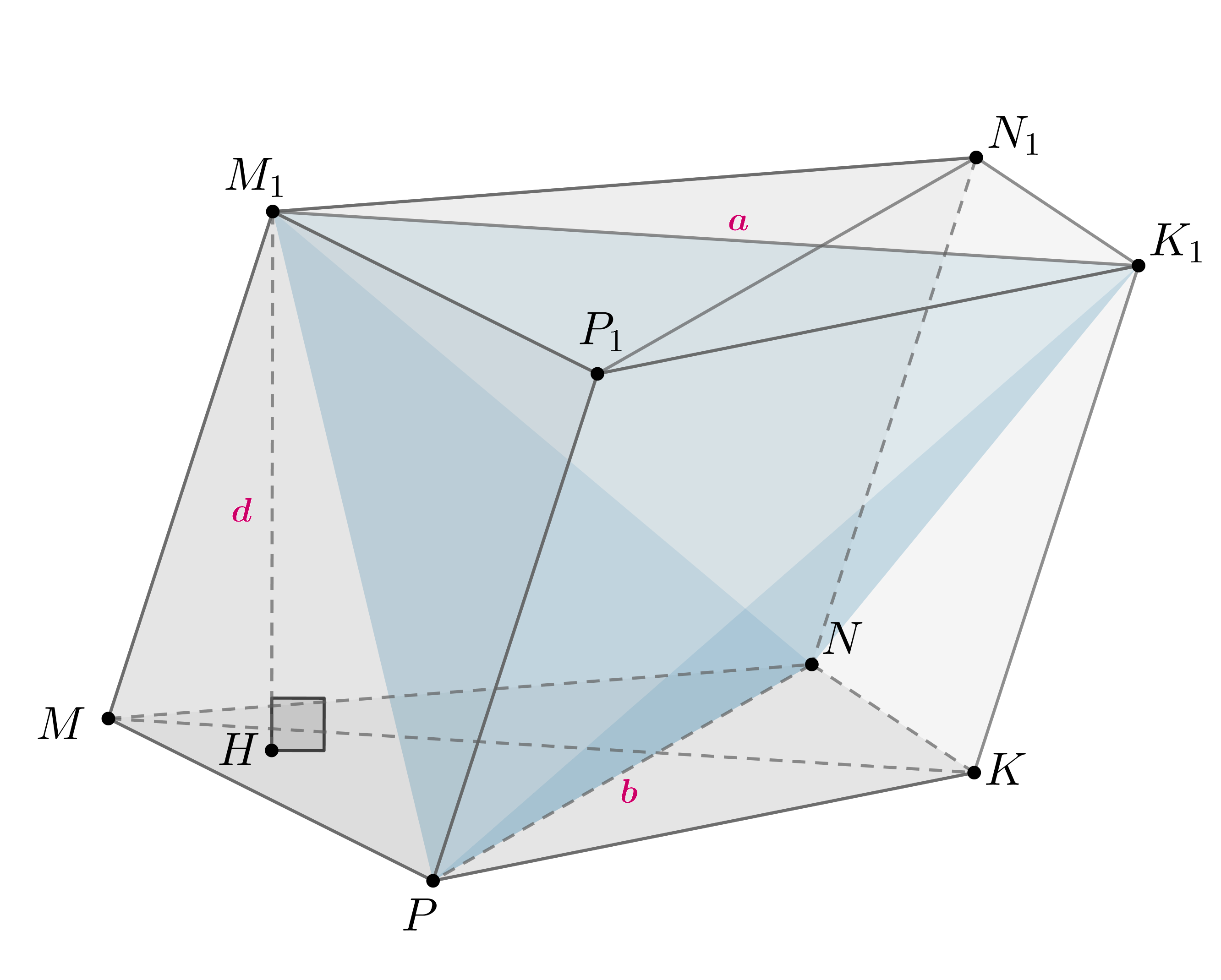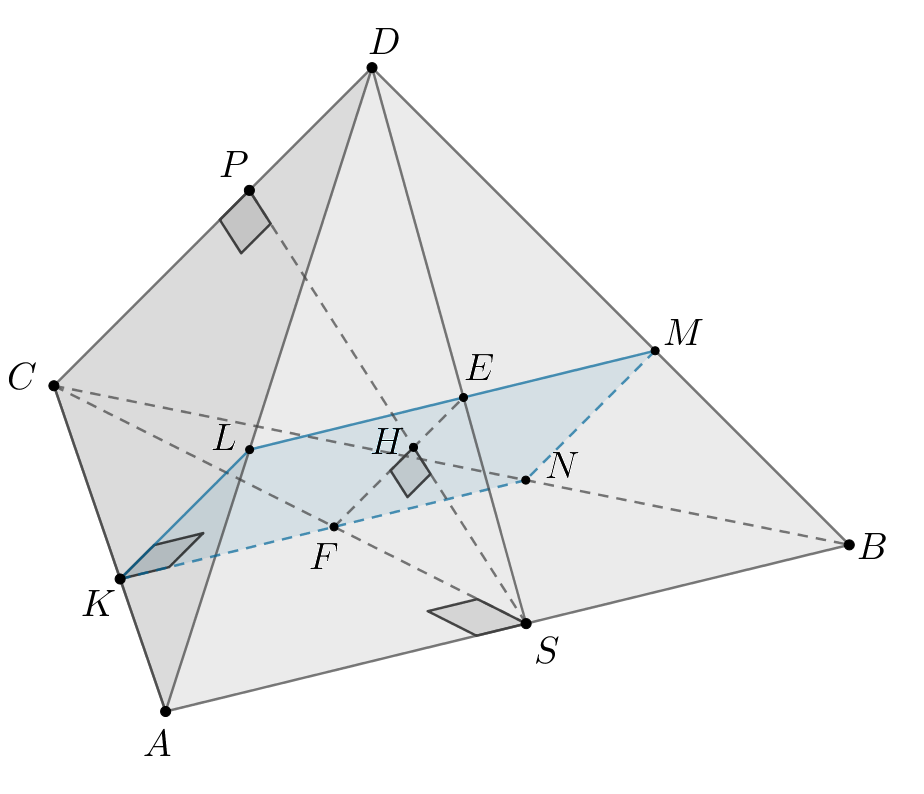Ответ: Заметим, что так как
 то расстояние от любой точки прямой  до этой плоскости будет одинаковым. Аналогично, так как  то расстояние от любой точки прямой  до этой плоскости будет одинаковым. Найдем расстояние от прямой  до этой плоскости. Оно будет являться высотой пирамиды  Проведем  Тогда  Проведем  Пусть  Далее имеем:  Тогда  и  — искомое расстояние. Из  следует, что  Аналогично получаем  Из доказанной формулы следует, что объем тетраэдра  равен  По теореме Фалеса имеем:  Отсюда получаем  Следовательно, объем пирамиды  равен  | |
