Решить задачу
| 24.04.2025, 19:37 | |
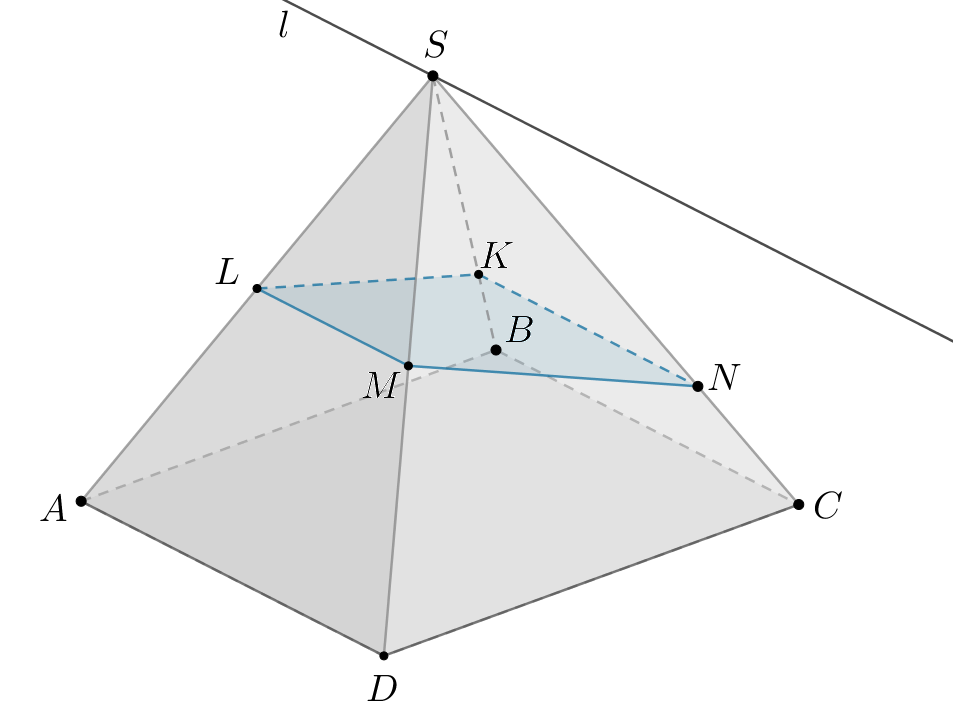
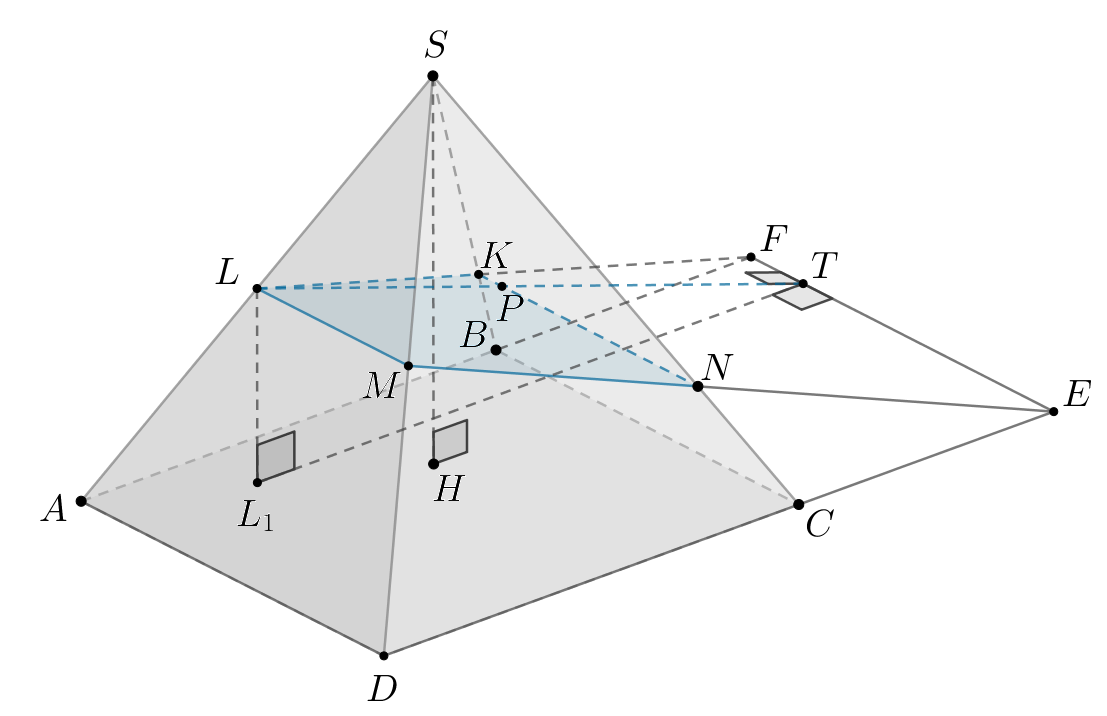
Дана пирамида а) Докажите, что б) Известно, что угол между плоскостью трапеции | |
|
| |
| Просмотров: 9 | | |
в основании которой лежит квадрат 
Сечение пирамиды — четырехугольник 
причем точки 
лежат на ребрах 
и 
соответственно. Известно, что 
и 
— середины ребер 
и 
а 
— трапеция и основания трапеции относятся как 
и плоскостью основания 
равен 
Найдите высоту пирамиды 
если площадь квадрата 
равна 32, а площадь четырехугольника 
равна 
| Всего комментариев: 2 | |
0
а) Будем пользоваться следующей теоремой: если нам даны три попарно пересекающиеся плоскости, то их линии пересечения либо параллельны, либо все пересекаются в одной точке. Из этой теоремы следует, что если две из трех линий пересечения параллельны, то третья линия пересечения также им параллельна.
 Так как  — линия пересечения плоскостей  и   — линия пересечения плоскостей  и  и  то  — линия пересечения плоскостей  и  — параллельна  Теперь рассмотрим три плоскости:   и  Так как  и  — середины  и  то  следовательно, линия пересечения плоскостей  и  — прямая  Тогда по теореме Фалеса  Далее имеем:   значит,  Но по условию  — квадрат, следовательно,  следовательно,  откуда следует, что  — трапеция. Также отсюда следует, что  Что и требовалось доказать.
0
б) Рассмотрим три плоскости
  и  и их линии пересечения   и  Так как  то  Пусть   Проведем  и  Тогда по теореме о трех перпендикулярах  Следовательно,   Пусть  Тогда так как  то  следовательно,  — высота трапеции  По теореме Фалеса  Найдем последнее отношение. По теореме Менелая для  и прямой  имеем:  Ответ: Следовательно,
 По теореме Менелая для  и прямой  имеем:  Следовательно,  значит,  Проведем  Тогда  следовательно,  — искомая высота. Пусть  Тогда  Так как  то  Следовательно,  Также заметим, что из  следует, что  Тогда  | |
