Решить задачу
| 24.04.2025, 19:38 | |
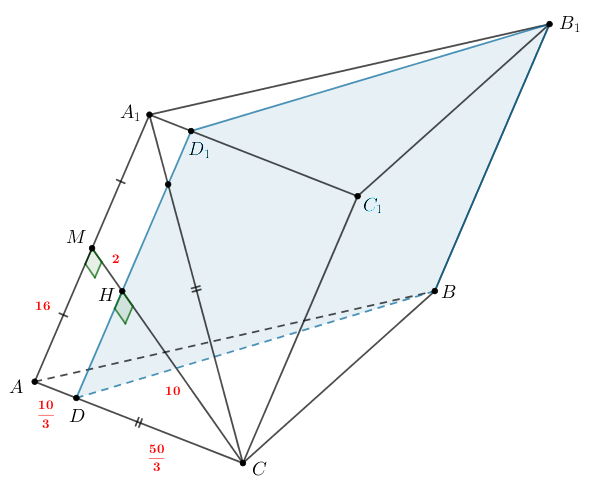
Дана треугольная призма а) Докажите, что одна из диагоналей грани б) Найдите расстояние от точки | |
|
| |
| Просмотров: 6 | | |
Точка 
— середина ребра 
Плоскость 
проходит через ребро 
и перпендикулярна прямой 
равна одной из ее сторон.
до плоскости 
если 
делит ребро 
в отношении 
считая от точки 
и 
| Всего комментариев: 2 | |
0
а) По условию
 Если прямая перпендикулярна плоскости, то она перпендикулярна каждой прямой, лежащей в этой плоскости, в частности,  Так как  — призма, то  следовательно,  Рассмотрим треугольник  в одноименной плоскости. Отрезок  является его медианой и высотой, значит,  — равнобедренный, то есть  Таким образом, в грани  диагональ  равна стороне  
0
б) Пусть плоскость
 пересекает прямую  в точке  прямую  — в точке  , прямую  — в точке  Заметим, что все эти три точки лежат в грани  Значит, они лежат на прямой пересечения грани  плоскостью  Нам нужно найти расстояние от точки  до плоскости  то есть длину  так как  а  — точка пересечения  и  По условию имеем:  Отсюда получаем  По условию  значит,  Тогда  Ответ: Рассмотрим треугольники
 и  Они подобны, так как  — общий и  как соответственные углы, образованные параллельными прямыми  и  и секущей  Тогда имеем:  Найдем  По условию  — середина  значит,  Треугольник  — прямоугольный, тогда по теореме Пифагора:  Таким образом,  Отсюда  Теперь можем найти длину   | |
