Описанная окружность и вписанный четырехугольник
| 23.04.2025, 10:32 | |
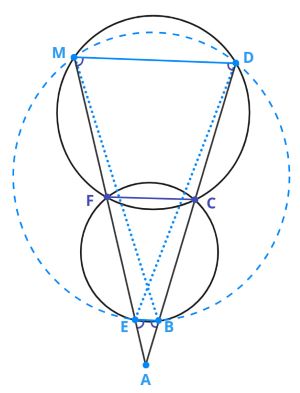
А вот и вторая геометрическая задачка из воспоминаний Деда Мороза: Две окружности разных радиусов пересекаются в точках а) Докажите, что б) Найдите сумму произведений длин противоположных сторон четырехугольника | |
|
| |
| Просмотров: 6 | | |
и 
причем их центры лежат по разные стороны от хорды 
Вне обеих окружностей взята точка 
лежащая по ту же сторону от хорды 
что и центр меньшей окружности. Прямая 
пересекает меньшую окружность в точках 
и 
а большую — в точках 
и 
Прямая 
пересекает меньшую окружность в точках 
и 
а большую — в точках 
и 
= 
если 
и 
| Всего комментариев: 1 | |
0
 а) Вспомним теорему о двух секущих и распишем ее для обеих окружностей. Для меньшей окружности справедливо:  откуда  Для большей окружности справедливо:  откуда  Из двух пропорций, в которых левые части одинаковы, выводим:   Ч.Т.Д. б) 1. В пункте а) мы доказали равенство:  Из него по обратной теореме Фалеса следует, что  и  2. Из подобия выводим равенства углов:  3. В условии пункта б) утверждается, что  С учетом с прошлых двух тождеств этот тезис дает понять, что  и  на самом деле равнобедренные. 4. Отсюда получаем, что трапеция  также равнобедренная. У любой равнобедренной трапеции сумма противоположных углов равна  следовательно, она вписанная. 5. Для вписанного четырехугольника справедлива теорема Птолемея, гласящая о том, что сумма произведений длин противоположных сторон вписанного четырехугольника равна произведению длин его диагоналей, то есть  NOTA BENE: Заметим, что теоремы Птолемея нет в учебниках федерального перечня, поэтому перед её применением на ЕГЭ следует привести её доказательство. Ответ: б) 1234 | |
