Подобие треугольников и пропорциональные отрезки
| 23.04.2025, 10:19 | |
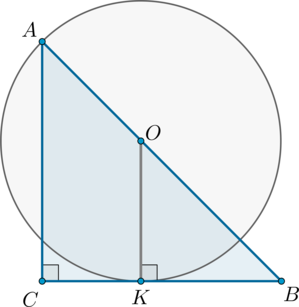
Окружность касается одного из катетов прямоугольного равнобедренного треугольника и проходит через вершину противолежащего острого угла. Найдите радиус окружности, если ее центр лежит на гипотенузе треугольника, а катет треугольника равен
(Источник: Сборник задач по геометрии, И.Ф.Шарыгин, Р.К.Гордин) | |
|
| |
| Просмотров: 6 | | |
.| Всего комментариев: 1 | |
0
В решении будем обозначать катет треугольника за
 . Пусть  – радиус окружности. Если  – точка касания окружности с катетом  , то  . Рассмотрим рисунок:  Заметим, что по двум углам  , следовательно,  Так как  , то  . По теореме Пифагора  . Так как  лежит на  , то  , следовательно,  . Тогда по теореме Пифагора из  : Так как  , то получаем Ответ:  | |
