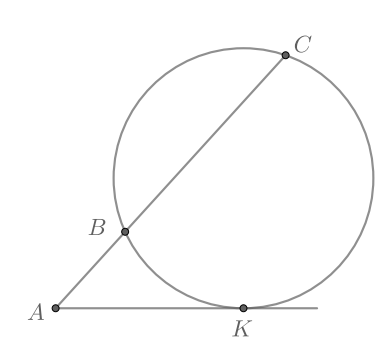
Касательные в точках  и  к окружности с центром  пересекаются под углом . Найдите угол . Ответ дайте в градусах.

Через точку  лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке  Другая прямая пересекает окружность в точках  и  причём   Найдите 

Хорды  и  окружности пересекаются в точке     Найдите 

Найдите площадь трапеции, диагонали которой равны 17 и 15, а средняя линия равна 4.

Найдите площадь трапеции, диагонали которой равны 10 и 8, а средняя линия равна 3.

В треугольнике  на его медиане  отмечена точка  так, что  Прямая  пересекает сторону  в точке  Найдите отношение площади треугольника  к площади четырёхугольника 

Середина  стороны  выпуклого четырёхугольника  равноудалена от всех его вершин. Найдите  если  а углы  и  четырёхугольника равны соответственно  и 

Касательные в точках  и  к окружности с центром в точке  пересекаются под углом  Найдите угол  Ответ дайте в градусах.

Середина  стороны  выпуклого четырёхугольника  равноудалена от всех его вершин. Найдите  если  а углы  и  четырехугольника равны соответственно  и 

В трапеции  боковая сторона  перпендикулярна основанию  Окружность проходит через точки  и  и касается прямой  в точке  Найдите расстояние от точки  до прямой  если  

Основания трапеции относятся как  Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?

Радиус вписанной в квадрат окружности равен  Найдите радиус окружности, описанной около этого квадрата.

Окружности радиусов 36 и 45 касаются внешним образом. Точки  и  лежат на первой окружности, точки  и  — на второй. При этом  и  — общие касательные окружностей. Найдите расстояние между прямыми  и 

Окружности радиусов 12 и 20 касаются внешним образом. Точки  и  лежат на первой окружности, точки  и  — на второй. При этом  и  — общие касательные окружностей. Найдите расстояние между прямыми  и 

Радиус окружности, описанной около квадрата, равен  Найдите радиус окружности, вписанной в этот квадрат.

В треугольнике  известны длины сторон   точка  — центр окружности, описанной около треугольника  Прямая  перпендикулярная прямой  пересекает сторону  в точке  Найдите 

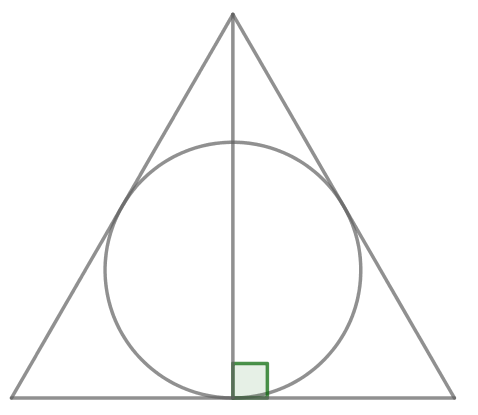
Радиус окружности, вписанной в равносторонний треугольник, равен 6. Найдите высоту этого треугольника.

В треугольнике  известны длины сторон   точка  — центр окружности, описанной около треугольника  Прямая  перпендикулярная прямой  пересекает сторону  в точке  Найдите 

Радиус окружности, вписанной в равносторонний треугольник, равен 15. Найдите высоту этого треугольника.

На стороне  остроугольного треугольника  как на диаметре построена полуокружность, пересекающая высоту  в точке     — точка пересечения высот треугольника  Найдите