Биссектрисы соседних углов четырехугольника пересекаются в середине его стороны. Докажите, что либо у этого четырехугольника равны два угла, либо две стороны параллельны.

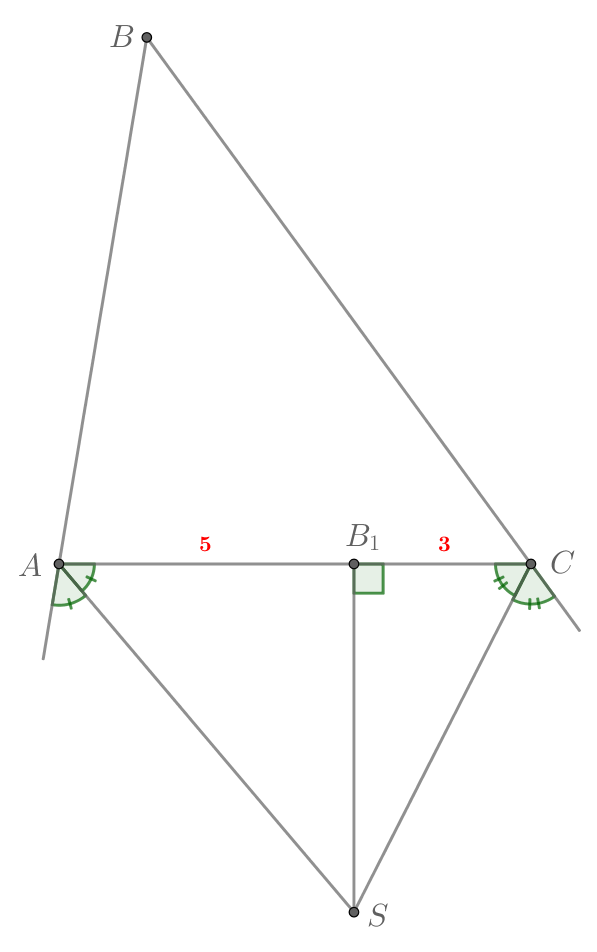
Провели биссектрисы двух внешних углов треугольника. Из точки их пересечения на его сторону опустили перпендикуляр. Он делит ее на отрезки с длинами 3 и 5. Найдите разность двух других сторон треугольника.

Через центр вписанной окружности треугольника провели прямую, параллельную одной из его сторон. Докажите, что эта прямая отсекает от данного треугольника меньший треугольник, периметр которого равен сумме двух сторон исходного треугольника.

В четырехугольнике  внешний угол при вершине  равен углу , . Докажите, что  — биссектриса угла .

Биссектрисы трех углов четырехугольника пересекаются в одной точке. Длины трех его сторон в указанном порядке равны 3, 4, 6. Найдите четвертую сторону.

Докажите, что биссектрисы двух внешних углов и третьего внутреннего угла треугольника пересекаются в одной точке.

Найдите геометрическое место точек, равноудалённых от двух пересекающихся прямых.

Биссектриса внешнего угла  треугольника  пересекает продолжение стороны  в точке  Докажите, что 

Докажите, что биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.

Найдите площадь трапеции с основаниями 11 и 4 и диагоналями 9 и 12.

Найдите площадь трапеции, параллельные стороны которой равны 16 и 44, а непараллельные — 17 и 25.

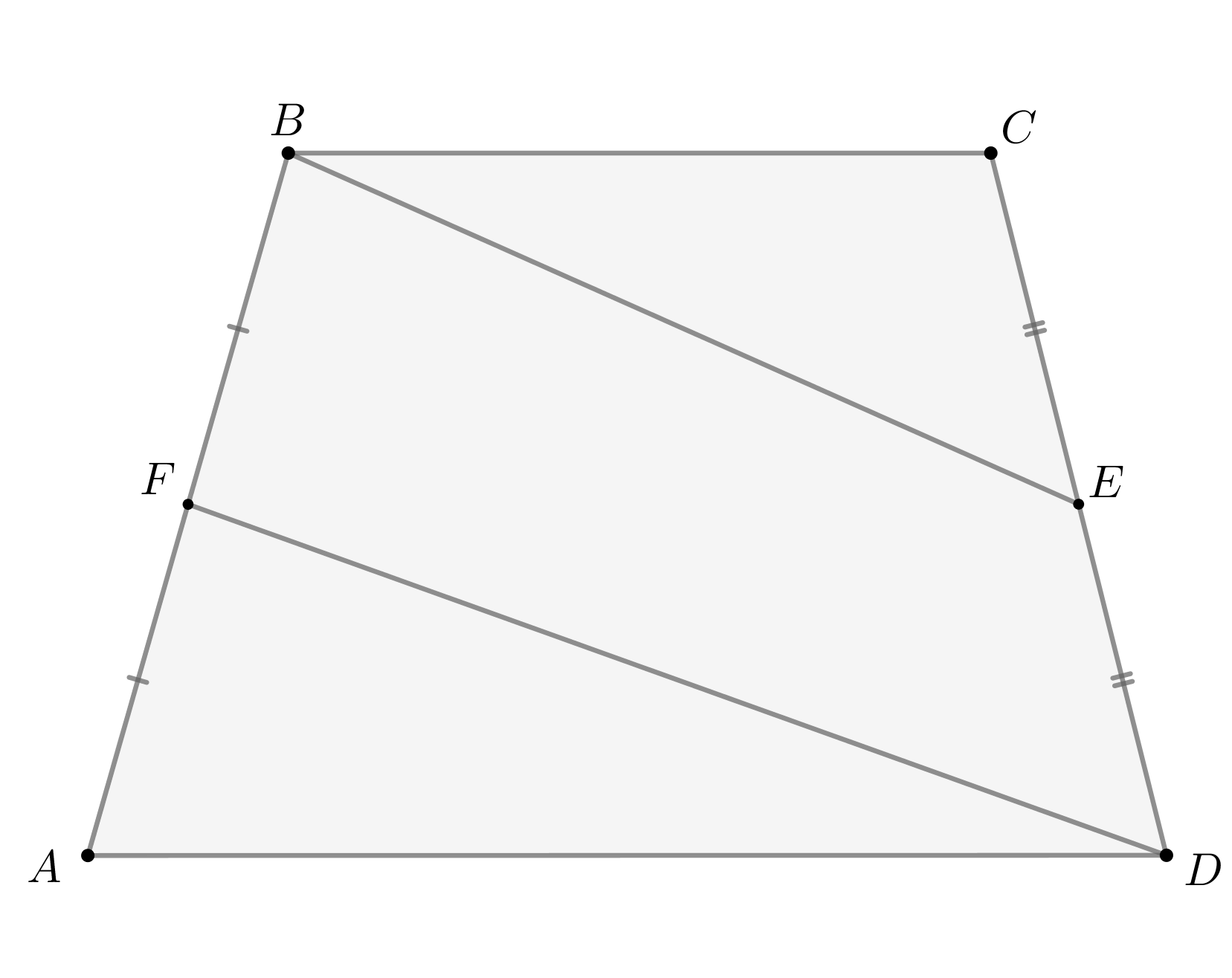
Середины боковых сторон трапеции соединили с ее вершинами так, как показано на рисунке. Могут ли полученные два отрезка лежать на параллельных прямых?

Вершину тупого угла  параллелограмма  соединили с серединой  его стороны . Высота  к основанию  параллелограмма пересекает отрезок  в точке . Найдите , если .

В трапеции  с основаниями  и  известно, что  и  Найдите основание 

Вершина  и середины сторон  и  параллелограмма  являются вершинами равностороннего треугольника. Найдите углы параллелограмма.

Трапеция  с основаниями  и  такова, что угол  — прямой и . Найдите отношение оснований 

Боковая сторона трапеции равна одному основанию и вдвое меньше другого основания. Докажите, что другая боковая сторона трапеции перпендикулярна одной из диагоналей.

Углы при одном из оснований трапеции равны  и , а длины оснований равны 2 и 3. Найдите боковую сторону, прилегающую к углу .

В трапеции  , , . Докажите, что .

Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.