Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если ее средняя линия равна 5.

Произвольную точку  внутри равностороннего треугольника  соединили с его вершинами. Докажите, что на каждой стороне треугольника можно выбрать по одной точке так, чтобы расстояния между этими точками были равны ,  и .

Основания равнобедренной трапеции равны  и  (), острый угол равен  Найдите площадь трапеции.

Основания трапеции равны 1 и 6, а диагонали — 3 и 5. Под каким углом видны основания из точки пересечения диагоналей?

В равнобедренной трапеции основания равны 40 и 24, а ее диагонали взаимно перпендикулярны. Найдите площадь трапеции.

Середина одной из боковых сторон трапеции равноудалена от двух не принадлежащих этой стороне вершин. Докажите, что трапеция прямоугольная.

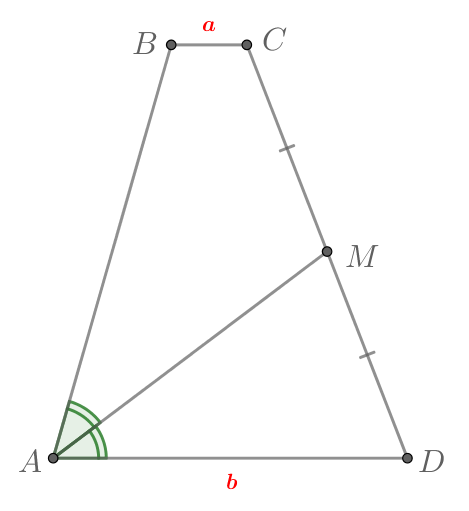
Биссектриса одного из углов трапеции делит ее боковую сторону пополам. Найдите другую боковую сторону трапеции, если основания равны  и 

Основания трапеции равны  и  где  Найдите длину отрезка, соединяющего середины диагоналей трапеции.

Диагональ равнобедренной трапеции равна 10 и образует угол  с основаниями трапеции. Найдите среднюю линию трапеции.

В треугольник со стороной  и высотой , проведенной к этой стороне, вписан квадрат таким образом, что две соседние вершины квадрата лежат на стороне , а две другие вершины квадрата лежат на двух других сторонах треугольника соответственно. Найдите периметр квадрата.

В квадрате  на стороне  взята точка  такая, что . Найдите расстояние от точки  до прямой .

В треугольник вписан ромб таким образом, что один угол у них общий, а противоположная вершина ромба лежит на стороне треугольника и делит ее на отрезки длинами  и . Найдите периметр треугольника, если сторона ромба равна .

Окружность касается одного из катетов прямоугольного равнобедренного треугольника и проходит через вершину противолежащего острого угла. Найдите радиус окружности, если ее центр лежит на гипотенузе треугольника, а катет треугольника равен .

(Источник: Сборник задач по геометрии, И.Ф.Шарыгин, Р.К.Гордин)

В параллелограмме  точка  — середина  а точка  — середина  Найдите отношение длин отрезков, на которые прямые  и  разделили диагональ 

В треугольнике  чевиана  делит сторону  на отрезки  и  Известно, что  Найдите 

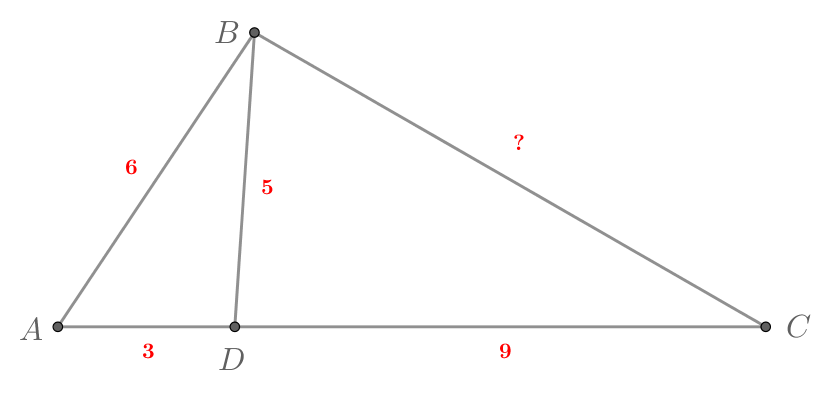
Найдите неизвестную сторону треугольника на картинке.

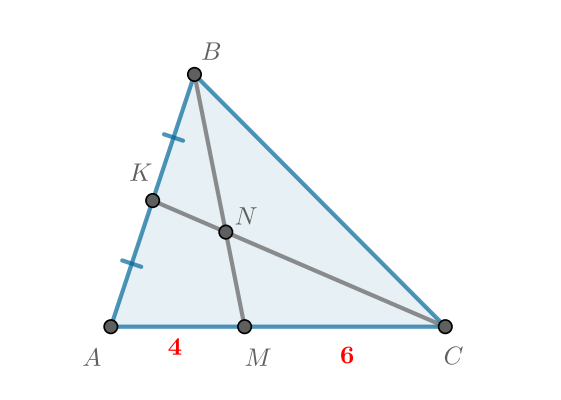
Найдите отношение 

В трапеции основания равны 18 и 12, а боковые стороны 15 и 12. Боковые стороны продолжили до взаимного пересечения. Найдите сумму длин отрезков, на которые продолжены боковые стороны.

В треугольнике  на середине стороны  отмечена точка  Точка  на продолжении стороны  за точку  такова, что  Найдите меньший из отрезков, на которые прямая  делит сторону  если 

В пятиугольнике  углы  и  равны,   Докажите, что равны отрезки  и