|
|
|
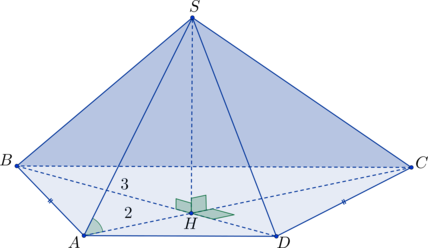
В основании пирамиды
|
|
Высота |
|
В пирамиде |
|
Дана пирамида |
|
Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
|
|
В основании пирамиды |
|
Плоскости |
|
Даны прямые |
|
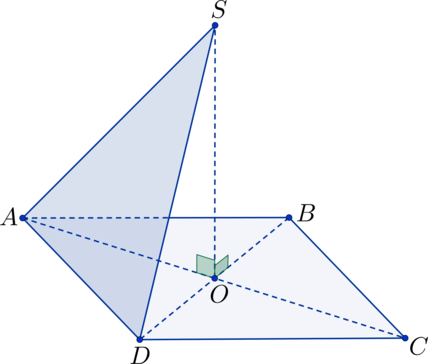
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите |
|
В квадрате |
|
Плоскости |
|
|
|
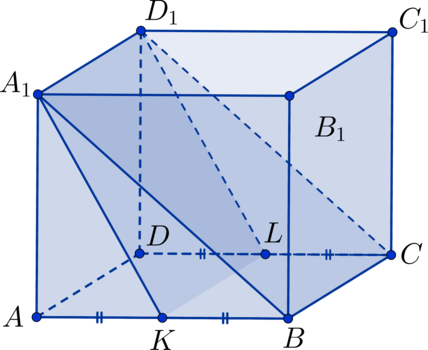
В кубе
|
|
В квадрате
|
|
Дан куб
|
|
Чему равен |
|
|
|
|
|
Дан треугольник |