|
Дана правильная четырехугольная пирамида, объем которой равен |
|
Пирамида
|
|
Дана правильная четырехугольная пирамида |
|
Дана правильная треугольная пирамида |
|
Дана правильная треугольная пирамида |
|
Дана правильная треугольная пирамида |
|
Найдите апофему в правильной шестиугольной пирамиде, если сторона шестиугольника равна |
|
Высота правильной треугольной пирамиды равна |
|
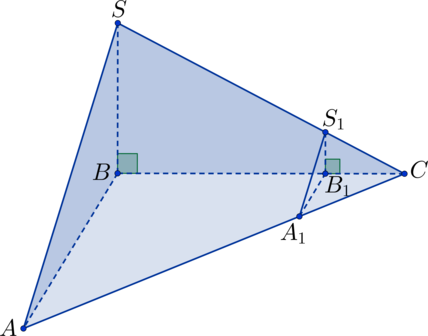
Дана прямоугольная пирамида |
|
Дана прямоугольная пирамида |
|
Найдите объем правильной четырехугольной пирамиды, если стороны основания равны |
|
Объем правильной четырехугольной пирамиды
|
|
Найдите объем правильной треугольной пирамиды, сторона основания которой равна 6, а высота равна
|
|
Найдите объем правильного тетраэдра, если одна из его апофем равна
|
|
В прямоугольной пирамиде
|
|
Объем правильной треугольной пирамиды равен |
|
Объем треугольной пирамиды равен 78. Через вершину пирамиды и среднюю линию ее основания проведена плоскость. Найдите объем отсеченной треугольной пирамиды.
|
|
В основании пирамиды |
|
|
|
|