Показано заданий: 2301-2320
|
Пусть
|
|
В параллелограмме
|
|
В параллелограмме
|
|
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
|
|
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении
|
|
В параллелограмме
|
|
В параллелограмме
|
|
В параллелограмме
|
|
В параллелограмме
|
|
В параллелограмме
|
|
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 6. Найдите его большую сторону.
|
|
Большая сторона параллелограмма равна
|
|
В параллелограмме
|
|
Из точки
|
|
Периметр параллелограмма равен 100, его большая сторона равна 32. Найдите меньшую сторону параллелограмма.
|
|
В параллелограмме
|
|
В параллелограмме
|
|
Один угол параллелограмма больше другого на
|
|
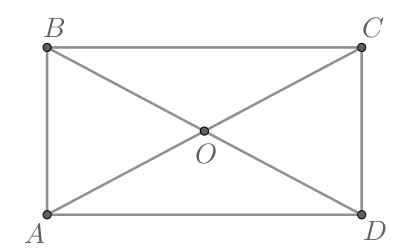
Диагонали параллелограмма
|
|
Периметр параллелограмма равен 15. При этом одна сторона этого параллелограмма на 5 больше другой. Найдите меньшую сторону параллелограмма.
|