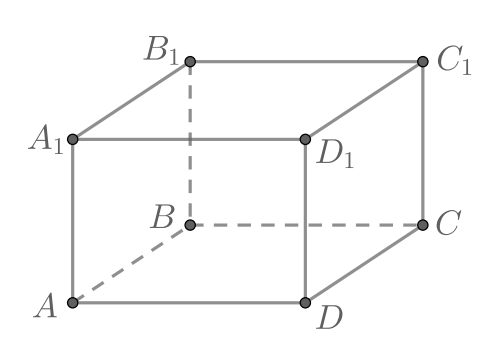
Дан прямоугольный параллелепипед, основания  и  которого являются квадратами со стороной . Пусть  – точка пересечения диагоналей грани ,  – точка пересечения диагоналей грани . Найдите .

Даны два прямоугольных параллелепипеда: ребра одного равны  и , а ребра другого равны  и . На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если .

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

Дан прямоугольный параллелепипед с ребрами  и . Найдите его диагональ.

В параллелепипеде  все грани представляют из себя ромбы с острым углом . Точки ,  и  принадлежат соответственно ребрам ,  и , причем , , . Найдите длину ломаной , если сторона ромба равна .
 

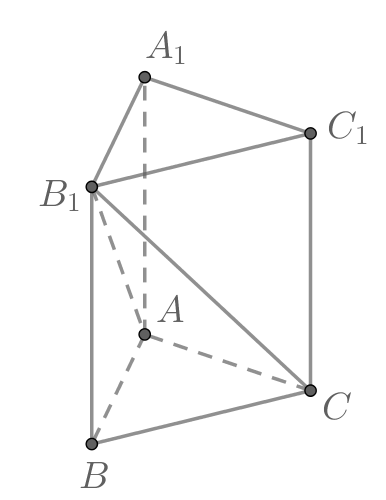
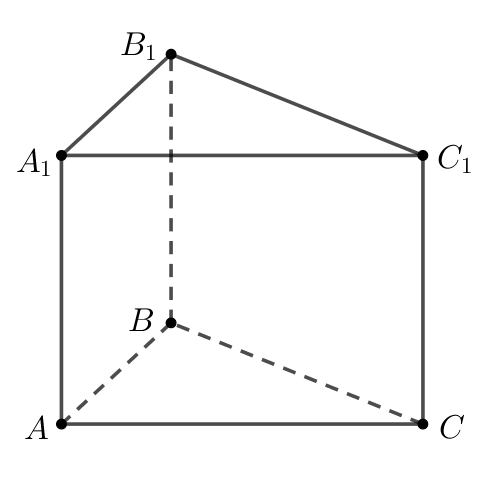
Найдите объем многогранника, вершинами которого являются точки , где  – параллелепипед, объем которого равен .

 — параллелепипед, точки  и  — середины рёбер  и  соответственно. Известно, что объём тела  равен 1. Найдите объём 

Найдите объём многогранника, вершинами которого являются вершины  правильной шестиугольной призмы  площадь основания которой равна 6, а боковое ребро 3.

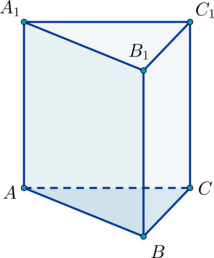
Дана правильная треугольная призма  площадь основания которой равна 8, а боковое ребро равно 6. Найдите объем многогранника, вершинами которого являются точки     

Через среднюю линию основания правильной треугольной призмы, объём которой равен 84, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.

Дана прямая призма , в основании которой лежит равнобедренная описанная около окружности трапеция  с боковой стороной , равной . Боковое ребро призмы равно . Отрезок  перпендикулярен прямой  и равен , причем  лежит на прямой . Найдите объем призмы.

Диагональ правильной четырехугольной призмы равна  и составляет с плоскостью боковой грани угол . Найдите объем призмы.

Дана прямая призма , в основании которой лежит равнобедренная трапеция , у которой , а острый угол при основании  равен . Пусть  – точка пересечения продолжений боковых сторон основания призмы. Найдите, отношение объема призмы  к объему прямой призмы, основанием которой является треугольник , если эти призмы имеют равные высоты.

Дана прямая призма, в основании которой лежит равнобедренная описанная около окружности трапеция  с боковой стороной, равной , и высотой, равной . Боковое ребро призмы равно . Найдите площадь полной поверхности призмы.

Дана правильная четырехугольная призма, диагональ которой равна , а диагональ основания равна . Найдите площадь полной поверхности призмы.

В прямой треугольной призме все боковые грани являются квадратами со стороной . Найдите объем призмы.

Найдите объём многогранника, вершинами которого являются вершины  правильной треугольной призмы  При этом площадь основания призмы равна 9, а боковое ребро равно 4.

Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

Найдите объем многогранника, вершинами которого являются точки     правильной треугольной призмы  площадь основания которой равна 6, а боковое ребро равно 9.

Площадь боковой поверхности треугольной призмы равна 36. Через среднюю линию основания этой призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсечённой треугольной призмы.