Показано заданий: 2241-2260
|
|
|
В окружности с центром
|
|
Хорда
|
|
Дуга окружности
|
|
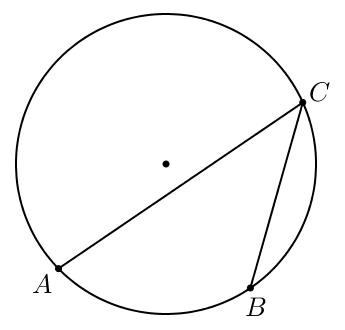
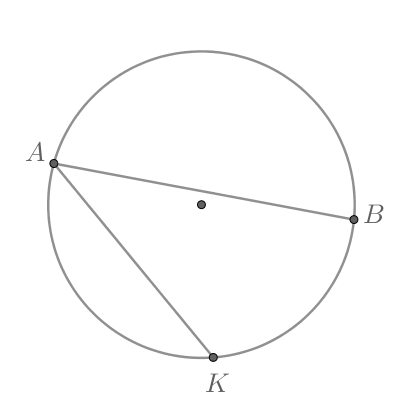
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
|
|
Из точки
|
|
На рисунке
|
|
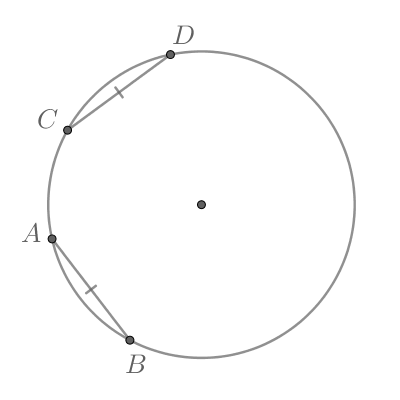
На окружности в следующем порядке отмечены четыре точки:
|
|
Точки
|
|
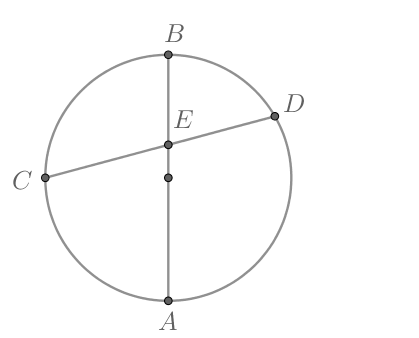
Хорды
|
|
Точки |
|
Основания равнобедренной трапеции равны
|
|
В равнобедренной трапеции основания равны
|
|
Основания равнобедренной трапеции равны
|
|
Основания равнобедренной трапеции равны
|
|
Проекция диагонали равнобедренной трапеции на ее большее основание равна
|
|
Найдите диагонали равнобедренной трапеции, если они перпендикулярны, а площадь трапеции равна
|
|
В равнобедренной трапеции
|
|
Диагонали в равнобедренной трапеции
|
|
В трапеции
|