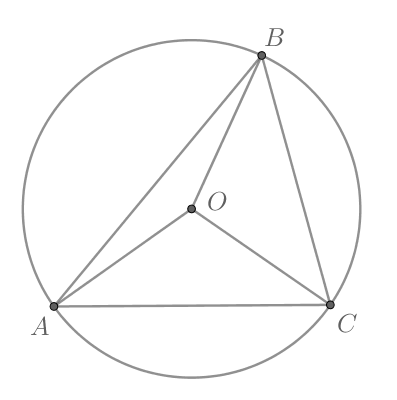
Длина окружности с центром в точке  равна 12.  точки  и  лежат на окружности и разбивают её на две дуги. Во сколько раз длина большей из получившихся дуг превосходит длину меньшей?

В треугольнике  известно, что  угол  равен  Найдите радиус вписанной окружности.

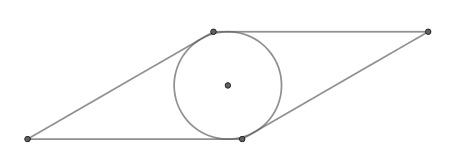
Сторона ромба равна  острый угол равен  Найдите радиус окружности, вписанной в этот ромб.

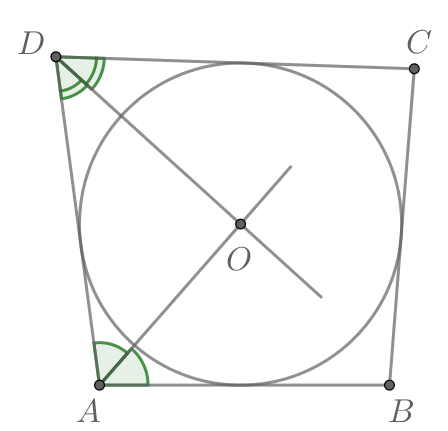
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как  Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 54.

В ромб со стороной  вписана окружность. Найдите радиус этой окружности, если площадь ромба равна 

Окружность вписана в угол  равный  Найдите расстояние от вершины угла до центра этой окружности, если расстояние между точками касания окружности и сторон угла равно 

Окружность  касается стороны  и продолжений сторон  и  треугольника  Найдите длину отрезка касательной к окружности  проведенной из точки  если периметр треугольника  равен 

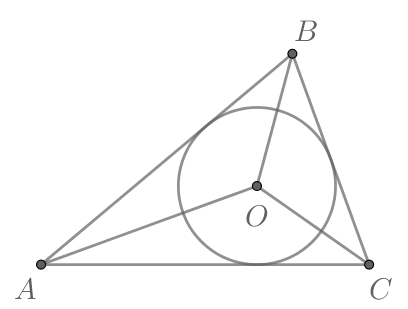
В треугольник вписана окружность радиуса  Одна из сторон треугольника равна  а разность двух других равна  Найдите большую сторону этого треугольника.

В треугольник  вписана окружность с центром в точке  причем   Найдите  Ответ дайте в градусах.

В четырёхугольнике      точка  лежит на биссектрисах углов  и  Найдите разность расстояний от точки  до  и от точки  до 

В четырёхугольник  вписана окружность,    Найдите длину 

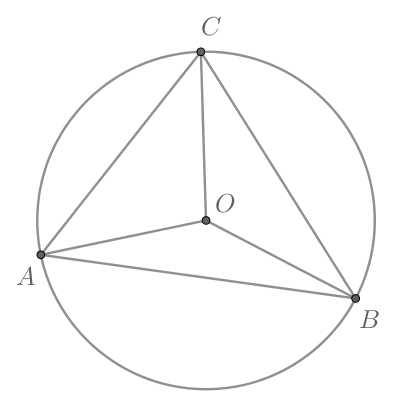
В окружность вписан пятиугольник  причем   Найдите  Ответ дайте в градусах.

Радиус описанной около четырехугольника  окружности равен  Найдите площадь этого четырехугольника, если известно, что все его стороны равны.

Во вписанном четырехугольнике  противоположные стороны попарно равны  и  Найдите радиус описанной около этого четырехугольника окружности.

Около треугольника  описана окружность с центром в точке   Найдите  Ответ дайте в градусах.

Около треугольника  описана окружность с центром в точке   Найдите  Ответ дайте в градусах.

Четырёхугольник  вписан в окружность. Угол  равен  угол  равен  Найдите угол  Ответ дайте в градусах.

Угол  четырехугольника  вписанного в окружность, равен  Найдите угол  этого четырехугольника. Ответ дайте в градусах.

Четырехугольник  вписан в окружность. Угол  равен  угол  равен  Найдите угол  Ответ дайте в градусах.

Два угла вписанного в окружность четырехугольника равны  и  Найдите больший из оставшихся углов. Ответ дайте в градусах.